现在优化一般不都是用牛顿法和梯度下降法吗?那上面那些算法还有什么用途吗?他们都各有什么特点?优缺点?
每一种算法的应用条件不一样。
很多算法在特别条件是已知中效果最好的,并不存在什么通用算法。
没有垃圾算法,只有不懂得使用的人。
当年神经网络也是垃圾算法,主要是不知道怎么用。
现在计算机中的垃圾算法,可能那天量子计算机普及了,在那种运行环境上可能是很好的算法。
有了电视,收音机并没有被淘汰。
有了核武器,但手枪并没有被淘汰。
各种算法就像数学公式一样,是一种思想,一种工具。像孙子兵法36计一样,真正能灵活运用的很少,每种算法都是一种策略,一种工具,看你怎么用。
你可能看不上的算法,如遗传算法,别人早用于生产系统了。
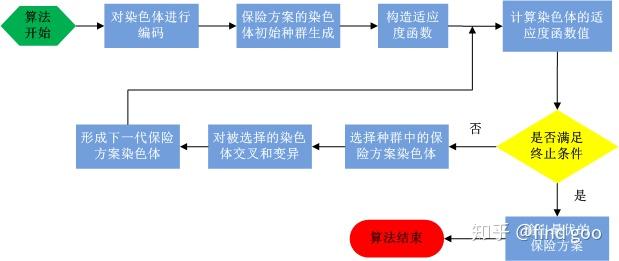
研究这两类算法完全是两拨人,一个是进化计算的领域,一个是数学优化领域,这两个领域都是解优化问题的,但是思路上有着本质的不同。所以经常会出现以下情景

领域之间的互相鄙视在学术界也是司空见惯,所以我们这里尽量不带有偏见的去分析一下两类方法的适用场景和优缺点对比(如有偏颇,欢迎指正)。
宏观的来说目前数学优化的应用场景要稍微广一些,所以我这里只列举出进化计算方法(模拟退火算法、粒子群优化算法、遗传算法和蚁群优化算法等)的主要适用场景。进化计算目前应用比较多的场景我个人的感觉有以下五个方面(除去这五个方面传统数学优化会应用的比较多一些):
神经网络超参数优化一直是一个经久不衰的话题,例如神经网络的训练算法的学习率,正则化参数,数据集minibatch的大小等等这些参数都属于超参数。超参数无疑对神经网络的效果有着极大的影响,传统的基于梯度的算法无法做超参数优化,因为根本无梯度可以求。所以目前主流的超参数优化方法有网格搜索 贝叶斯优化和进化计算。进化计算在超参数优化的问题上的效果还是不错的,相关的paper也很多。当然这里这里提到的神经网络也可以扩展到广义的机器学习模型。
神经网络结构优化,这个肯定是属于组合优化的问题,这类问题一般是NP-hard的(很难很难求解到精确解)。同样这类问题也是无梯度可求,基于梯度的方法不适用。所有多半是靠进化计算来做了。更多关于神经网络结构优化可参考 深度学习如何优化神经网络结构|架构?
进化计算在一部分组合优化问题和整数规划问题上表现比较好,甚至能够比肩传统的数学优化算法或者击败传统的数学优化算法。例如针对传统的VRP问题(车辆路径规划问题),在精巧的设计变异,交叉算子的情况下,遗传算法能够取得不错的效果。
有一部分优化问题由于其本身机理难以描述清楚或者其机理并不是一个解析解表达式的情况下,数学优化算法往往不适用,此时就是进化计算比较适合的情况了。举例来说就是我以前研究过带有偏微分方程的约束的优化问题,很多非线性的偏微分方程没有解析解,因此整个偏微分方程就是一个黑箱一样的东西,给一个输入能到达输出,但是就是无法知道输入和输出的函数表达式,因此也就无法求导数了。例如飞机动力学模型的设计,汽车动力学模型的设计都是依赖于流体的偏微分方程,这种动力学优化问题一般来说也很难用数学优化方法去解。据我所知进化计算在这方面应用会比较多一些。
传统的数学优化算法还没法直接去处理多目标优化问题,都是将多目标转化为单目标之后处理。而进化计算的最大的优势是可以直接处理多目标优化问题。至于为啥直接处理多目标优化问题比较好,可以参考:多目标优化的意义是什么
进化算法只需计算目标函数的值即可,对优化问题本身的性质要求是非常低的,不会像数学优化算法往往依赖于一大堆的条件,例如是否为凸优化,目标函数是否可微,目标函数导数是否Lipschitz continuity等等。例如上面提到的汽车动力学模型的设计是带有流体偏微分方程约束的,此时你根本就不知道那个目标函数凸不凸,可导不可导。这一点是进化算法相对数学优化算法来说最大的一个优势,实际上同时也是进化算法一个劣势,因为不依赖问题的性质(problem-independent)对所有问题都好使往往意味着没有充分的利用不同问题的特性去进一步加速和优化算法(这里很具有哲学辩证思想的是有优点往往就会派生出缺点)。这样看来数学优化算法的条条框框实际上是划定了,数学优化算法的适用范围,出了这个范围好使不好使不知道,但是在这个范围内数学优化就能给出一个基本的理论保证。基于一些特定的组合优化的结构去设计的进化计算方法已经实际上引入了更多的关于问题本身的信息了。这也就是在一些组合优化问题上,进化计算能够比肩传统数学优化的原因。
结论:对问题结构确定的优化问题,有充分的关于优化问题的信息来利用的时候数学优化一般来说有优势,例如线性规划,二次规划,凸优化等等。反之,可能使用进化算法就会有优势。对于一些数学优化目前不能彻底解决的问题例如NP hard问题,进化算法也有很大的应用前景。更多的利用特定问题的结构去设计特定的进化计算算法必然能够提升进化计算的能力。
进化算法的计算速度比较慢一直是大家的共识,这一点也很好理解,每迭代一次都需要计算M次目标函数,M是种群规模一般是30-50左右。进化算法的前沿的研究方向其中一个就是针对大规模优化问题的(large-scale), 我也曾查阅过相关顶级期刊的论文发现进化算法里的large-scale的规模,一般决策变量几千维就是large-scale的了。对数学优化算法来讲可能根本构不成large-scale。而实际问题中经常决策变量达到几百万以上的规模,此时进化计算的缺点就被暴露了。所以侧面反应出了进化算法在计算速度的瓶颈限制了其在大规模优化问题上的应用。
值得一提的是近几年来随着深度学习的崛起,人们对计算力的要求越来越高,基于GPU的并行计算和分布式计算的架构被广泛的应用到人工智能的各个领域。由于进化算法本身天生具有良好的并行特性,基于GPU并行计算的进化算法是否能够在一定程度上解决进化算法速度慢的问题绝对是一个值得研究的topic。
目前对于进化算法的理论性分析还停留在一个很初级的阶段,虽然有用动力学模型(微分方程)和随机过程的方法来证明进化算法的收敛性,但一般而言这类理论分析的假设条件过于强了,此类研究工作更多的倾向于是探索性的阶段,基本上很难真正的从理论上指导算法的设计。个人希望能够有更先进的数学工具来帮助进化算法完善理论分析方面的不足吧。与之相对的数学优化在算法收敛性分析,算法复杂度分析上已经比较完备了,并且其理论在一定程度上能够指导算法的设计。
综上所述,进化算法也好,数学优化也好都只是认识问题解决问题的工具之一,工具本身并不存在绝对的优劣之分,每种工具都有其适用的场景,辨别它们的长短,找到它们合适的应用场景是我们这些用工具的人应该做的。
更多关于进化计算和数学优化的内容可以参考
文雨之:【学界】数据+进化算法=数据驱动进化优化?进化计算PK 数学优化应用场景还是很多的,分两部分来说:
我研究生的课题就是和进化算法相关的,进化算法最主要的一个应用之一就包括高维数据最优值求解,包括经典的旅行商问题,路径规划问题等,这些都是可以通过进化算法来解决
如提问者所说,经典的BP神经网络是通过梯度下降来进行优化的,但是优化的结果取决于初始权重的设定、以及learning rate等参数的设定,所以训练的结果会存在不确定性,以及陷入局部最优,这个时候其实可以使用进化算法对参数进行调整,包括一开始的初始参数优化,或者可以通过模拟退火算法,神经网络的训练跳出局部最优的解空间。
最高票也提到了,当我们设计神经网络的模型的时候,通常会依据经验去确定其神经网络的结构,而没有更好的办法,是我们最终沦陷为调参boy。对于简单的神经网络而言,其结构的选择已经会对神经网络的训练结果会造成很大的影响了,更不要说深度神经网络,RNN、GAN等,而这种如果要人工调的话,真的就够呛了。这个时候进化算法就C为出道,他会在神经网络训练的过程中调整他的结构,并且不断的做出优化。综合上述两个优化方向,我们就可以对网络的参数和结构进行优化,这就变成了一个多目标问题。
现在各种不同的进化算法已经有很多了,基本把所有的动物都命名了一边,但是我觉得很多算法他其实都是有类似的思想的,而不同的算法适用于不同的问题和数据集,所以我觉得之后的趋势就是算法之前的融合。不去考虑用什么算法去解决什么问题,而是让算法在训练过程中评估需要用到什么方法,然后自行调用组合
其实我这个了解的不多,就拿我遇到的事情来说吧。需要处理资源调配、车辆调配的一些问题,当然在主流业务上都有专门的运筹优化工程师在做相关优化,但是很多业务上都是简单粗暴的调配的,所需要的代价可想而知。在公司今年的目标里会有很多类似的优化节约成本的目标,其实我觉得如果真的掌握了一些经典的进化算法,在合适的问题上加以应用,会有意想不到的收获。所以现在挺关注启发式算法在实际问题中的应用的。
脑子一热,噼里啪啦一通乱写,照道理应该要提供相关的引用证明的(一点也不严谨,但是谁让我懒)。应该也有写的不对的地方吧,如有问题望指正,多谢
用肯定是还在用的,但是总体上来说,这些方法已经算是比较原始的方法了,所以一般来说需要进行改进才能继续用下去,我总结了以下三类的算法改进:
三种类型的改进方法!
以下是我总结的改进算法的三种类型的方法和100多种已经改进的算法及相应的论文,供大家参考学习。
一、通过初始化种群改进
大多数群体智能算法初始种群中个体的生成是给定范围内随机生成,导致初始个体具有较大的随机性和不确定性,所以可以通过改进初始化种群的方式改进算法优化和收敛性能,实现局部开发和全局探索能力的提升。
1. 混沌映射
常见的混沌映射汇总_风吹乱了我的秀发-CSDN博客2. 反向学习
1.基于反向学习的种群初始化策略_feijingguan_wx的博客-CSDN博客_反向学习3. 莱维飞行
袁岚峰:苍蝇为啥难打?原来它们用了高等数学的风骚走位 | 把科学带回家二、策略优化个体迭代更新
每个群智能算法中的个体的寻优方式不一样,导致了每种算法的寻优能力不同,例如传统的鲸鱼优化算法中鲸鱼群分为三步:收缩包围,螺旋气泡捕食,随机搜索。但仅有这三步很容易陷入局部最优或者偏离目标。这个时候就需要多加上一到两步的寻优策略,来减小寻优时候所产生的误差,常加的策略有以下几种:
1.高斯游走策略(正态分布)
透彻理解高斯分布2. 随机游走策略(布朗运动)
石川:布朗运动、伊藤引理、BS 公式(前篇)3.正余弦优化策略
正弦余弦优化算法[记录]_weixin_Qingliang的博客-CSDN博客_正余弦优化算法4.自适应策略
自适应搜索策略_百度百科5.变异扰动策略
这一块我没找到相应的解释,我给大家解释一下什么是变异扰动,当算法进入末尾的时候一般会进入到一个局部搜索的状态,这个时候如果前期偏离了目标值,再怎么在局部进行寻优都是无效的,所以为了保障在最后寻优阶段能再跳出一次局部区域,可以将搜索群体随机弹跳到离目前所在位置较远的新区域,以此来检查是否还有更优的目标解,达到全局开发的效果,这无疑是种不错的改进方式,变异扰动的方法有,柯西变异、差分变异等扰动。
三、混合算法
有些优化算法适用于筛选,有些算法的群体则更易于扩散,这样的两种优化算法都有自己的优点,那么可以将两个算法的优点进行结合,使得新算法不仅筛选能力强,扩散性能也很好。
将两种算法的优点结合进行改进,如:
1. 遗传算法和粒子群算法结合的遗传粒子群算法(GAPSO)
2. 模拟退火算法和粒子群算法结合的遗传粒子群算法(SAPSO)
这篇里有100多种改进的群智能算法,对不知道该怎么改进的同学很有帮助!
论文中常用的改进群智能优化算法(100种改进算法、三类改进方法,干货收藏)最近我又为大家整理了50种科研中实用的工具,每个都可以直接拿来用~直接拿走~
冰河里的萌马:50个超实用的科研工具软件!研究生必看(建议收藏)智能优化算法笔记(一)
优化算法可以大体上分为两类:梯度下降算法和智能算法(粒子群、基因、蚁群、模拟退火等等)。
梯度下降算法的核心思想是:按照梯度方向(或反方向)寻找最优点。因为在数学上可以证明:梯度是函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大。
智能算法的核心思想则是:智能仿真。模仿自然界中的某些现象来寻找最优解,比如蚁群寻找食物,基因优胜劣汰等等。
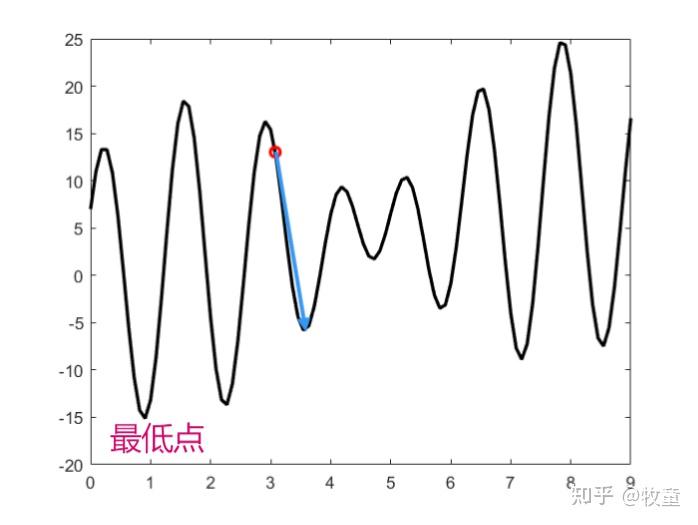
梯度优化算法在寻优的过程中存在着一个致命缺陷——容易陷入局部最优,它没有跳出局部最优点的能力。如图所示:红色的点只能沿着梯度方向(蓝色箭头)到达一个局部最优(波谷),没有跳出这个波谷来寻找最低点的能力。
为了解决这个问题,只能增加初始点的数量,即我只要撒上足够多的(红色)初始点,总有一个能够找到全局最优点(最低点),但是这样会带来两个问题:
- 计算效率太低(点越多,越有可能找到最低点,也越有可能带来计算资源的浪费)
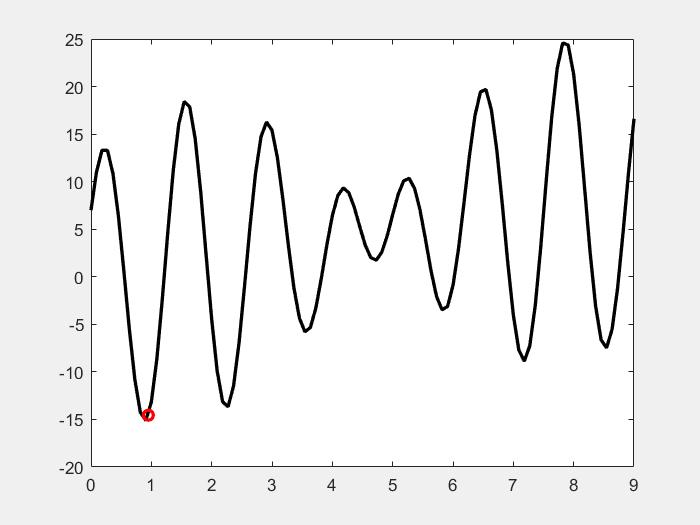
- 事先并不知道需要多少个初始点:下图只有7个谷底,在【0,9】上随机生成100个初始点,就能够大概率保证每次都能找到最低点;但是如果有50个局部最优解,那么100个初始点就显然不够用。而在寻优之前,我们显然是不知道有多少个局部最优解,这样,初始点太多就会造成计算资源的浪费,而初始点不够就会找不到全局最优解。
为了解决梯度下降算法的这两个问题,有学者提出了模拟退火算法。模拟退火算法的优势在于:能够更加经济地,在存在多个局部最优的目标函数中,找到全局最优解。
模拟退火算法的核心思想就是:先对初始点添加一个随机扰动,再判断是否接受该改变。
判断条件为:
- 若扰动后的点比原始点更小(朝优化方向移动),100%接受
- 若扰动后的点比原始点更大(朝优化反方向移动),以概率P接受
在弄明白P为多少之前,我们得先了解一点工业退火原理:退火就是将金属升温后,再缓慢降温,从而让金属内部分子排列更加紧密,以达到提升金属性能的一个加工工艺过程。
在升温过程中,金属粒子会加速随机移动;而随着温度按照特定曲线缓慢降低,金属粒子又会找到一个内能最低(粒子排列最为紧密)的排列方式。
式中:P为概率, 为内能的改变量,T为温度,k为常数。
在模拟退火算法中,就是参考了上述公式, 把 替换为
(函数值的改变量),取
,来计算概率P。
根据这个公式,我们可以得出如下结论:
- T越大,P越大,即温度越高,接受‘错误’扰动的概率越大
- T越小,P越小,即温度越低,接受‘错误’扰动的概率越小
模拟退火算法中的扰动大小与温度T成正比,即温度越高,扰动步长越大;即温度越低,扰动步长越小。
因此,模拟退火算法中的核心思想就是:
- 温度越高,接受‘错误’扰动的概率越大,扰动步长越大
- 温度越低,接受‘错误’扰动的概率越小,扰动步长越小
即:前期凭借扰动搜寻更多的新区域;后期收敛于局部最优解。如下图所示:
模拟退火算法由两个循环构成:外循环——>降温过程、内循环——>在该温度下的扰动
外循环:降温通常采用指数函数,即 ,
为降温系数(通常取0.85-0.99)
内循环:先生成随机扰动,再判断扰动是否接受(‘正确’100% 接受,‘错误’以P概率接受)
详细过程就不一一赘叙了,代码贴在下面,需要自取。
%% 一维模拟退火优化算法
clc;
clear;
%% 基本参数
% 外循环,降温过程
T_initial=100; %初始温度
alpha=0.9; %降温系数
T_min=1e-3; %最低温度
len=100; %迭代次数
% 内循环,迭代新解
cnt=100; %样本数量
x_min=0;
x_max=9;
x_initial=9 * rand(cnt,1);
%%
x=x_initial;
record_x=zeros(len+1,1);
record_x(1)=x(1);
for i=1:len
Temp=T_initial * alpha^(i-1);
if(Temp < T_min)
break;
end
for j=1:cnt
x(j)=m(x(j),Temp,x_min,x_max,T_initial);
end
record_x(i+1)=x(1);
record_y=f1(record_x);
y=f1(x);
[y_best,x_cnt]=min(y);
x_best=x(x_cnt);
end
%% gif
fig=figure;
% 生成轨迹
Tx=linspace(0, 9, 100);
Ty=f1(Tx);
plot(Tx, Ty, 'k', 'LineWidth', 2);
hold on
plt=plot(record_x(1), record_y(1),'ro','LineWidth', 2);
hold off
im=cell(1, length(x));
for i=1 : length(x)
plt.XData=record_x(i);
plt.YData=record_y(i);
% 暂停以显示动态过程
pause(0.3);
% 注释下面两句话可以看到动态输出
frame=getframe(fig);
im{i}=frame2im(frame);
end
% filename='D:\\桌面文件\\平时文件\\个人兴趣\\算法\\模拟退火\\1.gif';
% for idx=1:length(x)
% % 制作gif文件,图像必须是index索引图像
%[A, map]=rgb2ind(im{idx}, 256);
% if idx==1
% imwrite(A, map, filename, 'gif', 'LoopCount', Inf, 'DelayTime', 0.3);
% else
% imwrite(A, map, filename, 'gif', 'WriteMode', 'append', 'DelayTime', 0.3);
% end
% end
%% m函数
function[x]=m(x,T,x_min,x_max,T_initial)
y=f1(x);
while(true)
deta_x=(2*rand - 1) * T/T_initial * (x_max - x_min)/2;
x_new=x + deta_x;
if( (min(max(x_new,x_min),x_max)==x_new) )
break;
end
end
y_new=f1(x_new);
if(y_new < y)
x=x_new;
else
p=exp(-(y_new - y)/T);
if (rand < p)
x=x_new;
end
end
end
function f=f1(x)
f=x + 10*sin(5*x) + 7*cos(4*x);
end


